What if the Earth were made entirely of protons, and the Moon were made entirely of electrons?

—Noah Williams

This is, by far, the most destructive What-If scenario to date.

You might imagine an electron Moon orbiting a proton Earth, sort of like a gigantic hydrogen atom. On one level, it makes a kind of sense; after all, electrons orbit protons, and moons orbit planets. In fact, a planetary model of the atom was briefly popular (although it turned out not to be very useful for understanding atoms.[1]This model was (mostly) obsolete by the 1920s, but lived on in an elaborate foam-and-pipe-cleaner diorama I made in 6th grade science class.)

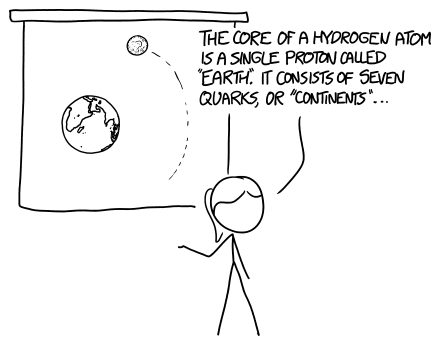
If you put two electrons together, they try to fly apart. Electrons are negatively charged, and the force of repulsion from this charge is about 20 orders of magnitude stronger than the force of gravity pulling them together.

If you put 10⁵² electrons together—to build a Moon—they push each other apart really hard. In fact, they push each other apart so hard, each electron would be shoved away with an unbelievable amount of energy.

It turns out that, for the proton Earth and electron Moon in Noah's scenario, the planetary model is even more wrong than usual. The Moon wouldn't orbit the Earth because they'd barely have a chance to influence each other;[2]I interpreted the question to mean that the Moon was replaced with a sphere of electrons the size and mass of the Moon, and ditto for the Earth. There are other interpretations, but practically speaking the end result is the same. the forces trying to blow each one apart would be far more powerful than any attractive force between the two.

If we ignore general relativity for a moment—we'll come back to it—we can calculate that the energy from these electrons all pushing on each other would be enough to accelerate all of them outward at near the speed of light.[3]But not past it; we're ignoring general relativity, but not special relativity. Accelerating particles to those speeds isn't unusual; a desktop particle accelerator can accelerate electrons to a reasonable fraction of the speed of light. But the electrons in Noah's Moon would each be carrying much, much more energy than those in a normal accelerator—orders of magnitude more than the Planck energy, which is itself many orders of magnitude larger than the energies we can reach in our largest accelerators. In other words, Noah's question takes us pretty far outside normal physics, into the highly theoretical realm of things like quantum gravity and string theory.

So I contacted Dr. Cindy Keeler, a string theorist with the Niels Bohr Institute. I explained Noah's scenario, and she was kind enough to offer some thoughts.

Dr. Keeler agreed that we shouldn't rely on any calculations that involve putting that much energy in each electron, since it's so far beyond what we're able to test in our accelerators. "I don't trust anything with energy per particle over the Planck scale. The most energy we've really observed is in cosmic rays; more than LHC by circa 10⁶, I think, but still not close to the Planck energy. Being a string theorist, I'm tempted to say something stringy would happen—but the truth is we just don't know."

Luckily, that's not the end of the story. Remember how we're ignoring general relativity? Well, this is one of the very, very rare situations where bringing in general relativity makes a problem easier to solve.

There's a huge amount of potential energy in this scenario—the energy that we imagined would blast all these electrons apart. That energy warps space and time just like mass does.[4]If we let the energy blast the electrons apart at near the speed of light, we'd see that energy actually take the form of mass, as the electrons gained mass relativistically. That is, until something stringy happened. The amount of energy in our electron Moon, it turns out, is about equal to the total mass and energy of the entire visible universe.

An entire universe worth of mass-energy—concentrated into the space of our (relatively small) Moon—would warp space-time so strongly that it would overpower even the repulsion of those 10⁵² electrons.

Dr. Keeler's diagnosis: "Yup, black hole." But this is no an ordinary black hole; it's a black hole with a lot of electric charge.[5]The proton Earth, which would also be part of this black hole, would reduce the charge, but since an Earth-mass of protons has much less charge than a Moon-mass of electrons, it doesn't affect the result much. And for that, you need a different set of equations—rather than the standard Schwarzschild equations, you need the Reissner–Nordström ones.

In a sense, the Reissner-Nordström equations compare the outward force of the charge to the inward pull of gravity. If the outward push from the charge is large enough, it's possible the event horizon surrounding the black hole can disappear completely. That would leave behind an infinitely-dense object from which light can escape—a naked singularity.

Once you have a naked singularity, physics starts breaking down in very big ways. Quantum mechanics and general relativity give absurd answers, and they're not even the same absurd answers. Some people have argued that the laws of physics don't allow that kind of situation to arise. As Dr. Keeler put it, "Nobody likes a naked singularity."

In the case of an electron Moon, the energy from all those electrons pushing on each other is so large that the gravitational pull wins, and our singularity would form a normal black hole. At least, "normal" in some sense; it would be a black hole as massive as the observable universe.[6]A black hole with the mass of the observable universe would have a radius of 13.8 billion light-years, and the universe is 13.8 billion years old, which has led some people to say "the Universe is a black hole!" (It's not.)

Would this black hole cause the universe to collapse? Hard to say. The answer depends on what the deal with dark energy is, and nobody knows what the deal with dark energy is.

But for now, at least, nearby galaxies would be safe. Since the gravitational influence of the black hole can only expand outward at the speed of light, much of the universe around us would remain blissfully unaware of our ridiculous electron experiment.

What if all of the sun's output of visible light were bundled up into a laser-like beam that had a diameter of around 1m once it reaches Earth?

—Max Schäfer

Here's the situation Max is describing:

If you were standing in the path of the beam, you would obviously die pretty quickly. You wouldn't really die of anything, in the traditional sense. You would just stop being biology and start being physics.

When the beam of light hit the atmosphere, it would heat a pocket of air to millions of degrees[1]Fahrenheit, Celsius, Rankine, or Kelvin—it doesn't really matter. in a fraction of a second. That air would turn to plasma and start dumping its heat as a flood of x-rays in all directions. Those x-rays would heat up the air around them, which would turn to plasma itself and start emitting infrared light. It would be like a hydrogen bomb going off, only much more violent.

This radiation would vaporize everything in sight, turn the surrounding atmosphere to plasma, and start stripping away the Earth's surface.

But let's imagine you were standing on the far side of the Earth. You're still definitely not going to make it—things don't turn out well for the Earth in this scenario—but what, exactly, would you die from?

The Earth is big enough to protect people on the other side—at least for a little bit—from Max's sunbeam, and the seismic waves from the destruction would take a while to propogate through the planet. But the Earth isn't a perfect shield. Those wouldn't be what killed you.

Instead, you would die from twilight.

The sky is dark at night^{[citation needed]} because the Sun is on the other side of the Earth.^{[citation needed]} But the night sky isn't always completely dark. There's a glow in the sky before sunrise and after sunset because, even with the Sun hidden, some of the light is bent around the surface by the atmosphere.

If the sunbeam hit the Earth, x-rays, thermal radiation, and everything in between would flood into the atmosphere, so we need to learn a little about how different kinds of light interact with air.

Normal light interacts with the atmosphere through Rayleigh scattering. You may have heard of Rayleigh scattering as the answer to "why is the sky blue." This is sort of true, but honestly, a better answer to this question might be "because air is blue." Sure, it appears blue for a bunch of physics reasons, but everything appears the color it is for a bunch of physics reasons.[2]When you ask, "Why is the statue of liberty green?" the answer is something like, "The outside of the statue is copper, so it used to be copper-colored. Over time, a layer of copper carbonate formed (through oxidation), and copper carbonate is green." You don't say "The statue is green because of frequency-specific absorption and scattering by surface molecules."

When air heats up, the electrons are stripped away from their atoms, turning it to plasma. The ongoing flood of radiation from the beam has to pass through this plasma, so we need to know how transparent plasma is to different kinds of light. At this point, I'd like to mention the 1964 paper Opacity Calculations: Past and Future, by Harris L. Mayer, which contains the single best opening paragraph to a physics paper I've ever seen:

Initial steps for this symposium began a few billion years ago. As soon as the stars were formed, opacities became one of the basic subjects determining the structure of the physical world in which we live. And more recently with the development of nuclear weapons operating at temperatures of stellar interiors, opacities become as well one of the basic subjects determining the processes by which we may all die.

Compared to air, the plasma is relatively transparent to x-rays. The x-rays would pass through the plasma, heating it through effects called Compton scattering and pair production, but would be stopped quickly when they reached the non-plasma air outside the bubble. However, the steady flow of x-rays from the growing pocket of superhot air closer to the beam would turn a steadily-growing bubble of air to plasma. The fresh plasma at the edge of the bubble would give off infrared radiation, which would head out toward the horizon (along with the infrared already on the way), heating whatever it finds there.

This bubble of heat and light would wrap around the Earth, heating the air and land as it went. As the air heated up, the scattering and emission from the plasma would cause the effects to propogate farther and farther around the horizon. Furthermore, the atmosphere around the beam's contact point would be blasted into space, where it would reflect the light back down around the horizon.

Exactly how quickly the radiation makes it around the Earth depends on many details of atmospheric scattering, but if the Moon happened to be half-full at the time, it might not even matter.

When Max's device kicked in, the Moon would go out, since the sunlight illuminating it would be captured and funneled into a beam. Slightly after the beam made contact with the atmosphere, the quarter moon would blink out.

When the beam from Max's device hit the Earth's atmosphere, the light from the contact point would illuminate the Moon. Depending on the Moon's position and where you were on the Earth, this reflected moonlight alone could be enough to burn you to death ...

... just as the twilight wrapped around the planet, bringing on one final sunrise.[3]Here's an image which is great for annoying a few specific groups of people:

There's one thing that might prevent the Earth's total destruction. Can Max's mechanism actually track a target? If not, the Earth could be saved by its own orbital motion. If the beam was restricted to aiming at a fixed point in the sky, it would only take the Earth about three minutes to move out of the way. Everyone on the surface would still be cooked, and much of the atmosphere and surface would be lost, but the bulk of the Earth's mass would probably remain as a charred husk.

The Sun's death ray would continue out into space. Years later, if it reached another planetary system, it would be too spread out to vaporize anything outright, but it would likely be bright enough to heat up the surfaces of the planets.

Max's scenario may have doomed Earth, but if it's any consolation, we wouldn't necessarily die alone.

What if I tried to re-enter the atmosphere in my car? (a 2000 VW Jetta TDI). Would it do more environmental damage than it is already apparently doing?

—Casey Berg

Believe it or not, throwing cars at a planet might be better for the planet than driving them on the surface. But it's hard to say for sure.

Volkswagen, as you've apparently heard, has been cheating on pollution tests since 2009. Your car was made before they started cheating, but that doesn't actually mean it pollutes less. Since the 1970s, the US has been tightening the rules around some of the exhaust gasses that create smog, like nitric oxide. By the mid-2000s, when the latest round of standards kicked in, Volkswagen apparently decided it was too expensive to keep up without sacrificing performance. Instead, they modified their cars to cheat on the tests, then lied to customers about how clean their cars were.

If you somehow put your car in orbit, then let it re-enter the atmosphere and burn up like a satellite, that would put an end to the tailpipe pollution.

On the other hand, burned fragments of your car (and body) would be scattered throughout the stratosphere. So what impact does space debris have on our air?

The surprising answer is that no one really knows. Roughly one major piece of space debris, like a satellite or booster rocket, re-enters the atmosphere each day. We talk about them "burning up," but they don't really disappear. Big chunks of them make it to the ground (usually falling in the ocean or landing in the desert somewhere.) Other dust and fragments are scattered throughout the stratosphere, and no one really knows what effect they have on anything.

Your car's shockwave would also create nitric oxide, which would—briefly—eat a small hole in the ozone layer. That hole would "close up" quickly, and the overall impact on the ozone layer would be small compared to other sources of ozone depletion.

While your car would briefly harm the ozone layer, it would help with global warming. I don't know how long you expect to have your car, but if you drive it another hundred thousand miles, it will emit about 20 or 30 tons of carbon dioxide. By destroying your car, it's true that you'll be literally putting carbon into the atmosphere, but not nearly as much as you would by continuing to drive it.

In the end, the real problem isn't the re-entry—it's the launch. Rocket launches have a much larger impact to the environment than re-entry, although it's still small in the grand scheme of things since we don't launch very many rockets.

Which raises a final question: What are you and your car doing in orbit in the first place? Are you the only one? Or have all cars been teleported into orbit? If so, we could be in trouble.

It's unlikely that any one piece of satellite debris will hit someone. But there are several hundred million passenger cars in the United States alone. If all of them were suddenly shot into orbit and allowed to reenter, it's likely that somewhere between a few hundred and a few thousand people would be injured or killed by falling engine blocks, transmissions, and half-melted axles.

On the other hand, about thirty thousand Americans are killed each year in motor vehicle accidents. So while launching all our cars into space—and letting them fall back down and hit us—might sound like a bad idea ...

... it's arguably a lot safer than continuing to drive them.

What if you built a siphon from the oceans on Europa to Earth? Would it flow once it's set up? (We have an idea for selling bottled Europa water.)

—A group of Google Search SREs

No, but I like where you're going with this.

Siphons are neat—they let you pump water up and over a barrier using just a tube and gravity. You can use siphoning to empty swimming pools, fill awkwardly-shaped containers, or get up to all kinds of trouble.[1]I asked some friends to suggest which thing in their house they'd be most upset to find someone siphoning water into. Answers included: Spice drawer, gumball machine, tea collection, bottle of vitamins, watercolor paint set, bag of rice with a cell phone in it, mint-condition instant oatmeal collection, carefully tuned musical glasses, ice hotel, prizewinning sand castle, sodium action figure collection, gremlin cage, Martian soil sample, dehydrated astronaut ice cream, and rack of those water-sensing self-inflating lifeboats.

It's not necessarily obvious at first glance, but siphoning works because of air pressure. Before we answer the Europa question, it may help to go over how siphons work.

If you take a tube full of water and point the ends down, gravity will try to pull the water down, making it fall out of both sides. If the water did start to fall out, a vacuum would form in the middle, since there's no way for air to get in to fill the gap. Each column of water would then have a vacuum on one side and air on the other, which means it would be pushed back up into the tube.

In reality, this doesn't happen; the air pressure stops the vacuum from opening up in the first place, and the water just sits there in the tube. Or, at least, it would if it were perfectly balanced.

If the water in one end is slightly lower than the other, then the column of water on that side pushes down harder against the air than the column on the other side. This imbalance causes the water to "tip" and run out of the heavier end.

To siphon something, you can just keep feeding more water into the tube on the higher side. As long as the surface of that water is higher up than the place where the water is coming out, the siphon will keep running.

If the column of water is more than about 34 feet[2]10 meters​[3]2 giraffes high, the pressure from the weight of the water becomes too strong for Earth's air pressure to counteract, and the water does fall out from both sides and briefly create a vacuum.[4]Although as the pressure drops, the water boils away to fill it, so you can't actually get too close to a pure vacuum this way. However, if you use something like olive oil (or mercury), you can get much closer. This means that on Earth's surface, you can't siphon water over a barrier that's more than 34 feet high. In Denver, where the air pressure is lower, the limit is 28 feet. In a vacuum—in theory—you can't siphon at all.[5]In practice, it turns out siphons do work in a vacuum, at least a little bit, because the "stickiness" of the water keeps it from pulling apart in the middle.

Europa has barely any atmosphere, so you won't be able to do much siphoning. But you also can't siphon water out of the atmosphere from a planet in general. A column of atmosphere, which is miles high, pushes down only as hard as a column of water 34 feet high. The water column is smaller because water is much denser than air. As long as the stuff on top is less dense than the liquid below it, you can't use the pressure from the stuff on top to siphon the liquid up above the stuff on top.[6]Most of the time, things sort themselves into layers, with the denser ones on the bottom. Occasionally, in the Earth, layers of dense rock will end up above layers of less-dense oil. This is why—when oil wellheads break—oil can sometimes come spurting out without any help from the pumps.

Even if you could generate a lot of pressure, pumping water from Europa's surface would take some work. Europa's gravity is weaker than Earth's, which means lifting something up from the surface of Europa takes less energy, but it's still not easy. The energy required to "climb out of Europa's gravity well" is the same as the energy required to climb up 209 kilometers against Earth's surface gravity. (Earth's gravity well, by comparison, is about 6,379 kilometers "deep"—click on this comic for an illustration.)

Once you've lifted the water out of Europa's gravity well, you then have to lift it the rest of the way out of Jupiter's, which is a lot deeper. Then, you have to do more work to push the water on a trajectory where it intercepts Earth. In terms of energy, the whole task is roughly equivalent to lifting the water about 2,500 kilometers in Earth gravity:

You could send the water to Earth by launching it from the surface of Europa at about 7 km/s. Conveniently, since Europa has no atmosphere, you don't need to use inefficient rockets to climb up to space. You can launch the water directly from the surface using something simpler, like a coilgun.

When the water reaches Earth, it can use atmospheric braking to slow down, and the individual bottles could be steered directly to their targets. Timing the deliveries would be tricky, sure, but it sure would be impressive if you got it right. Plus, you could totally one-up Amazon's drone delivery scheme.

At current electricity prices, the launch would cost a minimum of 50 cents (US) per bottle. Of course, getting electricity on Europa is probably a bit more expensive than getting it on Earth,[7]Or would need an awfully long cord. and setting up the purification plant and bottling operation on Europa wouldn't be cheap, to put it mildly.

All in all, you're going to have to charge an awful lot per bottle to break even on this whole operation. And if it turns out Europa's water has some weird alien pathogen in it, you might accidentally kill all your customers.[8]And, possibly, everyone else.

This may sound like your plan is pretty impractical and unrealistic, especially since there's no point to it all. Water is water. Once you've purified the water on Europa to make it drinkable, it won't be much different from water here on Earth. On the other hand, we ship water around the world from Fiji for no reason, so who knows. Maybe, with the right marketing, this idea could work.

How long would it take for a single person to fill up an entire swimming pool with their own saliva?

—Mary Griffin, 9th grade

The average kid produces about half a liter of saliva per day, according to the paper Estimation of the total saliva volume produced per day in five-year-old children, which I like to imagine was mailed to the Archives of Oral Biology in a slightly sticky, dripping envelope.

A five-year-old probably produces proportionally less saliva than a larger adult. On the other hand, I'm not comfortable betting that anyone produces more drool than a little kid, so let's be conservative and use the paper's figure.

If you're collecting your saliva,[1]This question is gross, by the way. you can't use it to eat.[2]I hope. You could get around this by chewing gum or something, to get your body to produce extra saliva, or just by drinking liquid food or getting an IV.

At the rate of 500 mL per day from the paper, it would take you about a year to fill a typical bathtub.

A bathtub full of saliva is pretty gross, but that's not what you asked about. For some reason—I don't really want to know why—you asked about filling a pool.

Let's imagine an Olympic-sized swimming pool, which is 25 meters by 50 meters. Depths vary, but we'll suppose this one is uniformly 4 feet deep,[3]You can read more of the regulations here; a pool with starting blocks does need a slightly deeper bit near each end, but it can be shallower in the middle. There doesn't seem to be anything in the rules about a maximum depth, so I suppose you can make a pool that continues through to the other side of the Earth, but then you run into trouble when you try to follow the instructions in section FR 2.14 about painting lane markings on the bottom. so you can probably stand up in it.

At 500 mL per day, it would take you 8,345 years to fill this pool. That's a long time for the rest of us to wait, so let's imagine you went back in time to get started on this project early.

8,345 years ago, the ice sheets that covered much of the northern parts of the world had mostly receded, and humans had just begun to develop agriculture. Let's imagine you started your project then.

By 4000 BCE, when the civilizations of the Fertile Crescent had begun to develop in modern-day Iraq, the saliva would be a foot deep, covering your feet and ankles.

By 3200 BCE, when writing was first developed, the saliva would creep past your knees.

Around the mid-2000s BCE, the Great Pyramid was constructed and early Mayan cultures emerged. At this point, the saliva would be getting close to your fingertips if you didn't lift your arms up.

Around 1600 BCE, the eruption of a huge volcano in the Greek island now known as Santorini caused a massive tsunami which devastated the Minoan civilization, possibly causing its final collapse. As this happened, the saliva would probably be approaching waist-deep.

The saliva would continue to rise throughout the next three millennia of history, and by the time of Europe's industrial revolution it would be chest-deep, easily enough saliva to swim in. The last 200 years would add the final 3 centimeters, and the pool would finally be filled.

It would take a long time, sure. But it would all be worth it, because at the end of it all, you'd have an Olympic-size swimming pool full of saliva. And isn't that, deep down, all any of us really want?[4]No. It is not.

Can you use a magnifying glass and moonlight to light a fire?

—Rogier Spoor

At first, this sounds like a pretty easy question.

A magnifying glass concentrates light on a small spot. As many mischevious kids can tell you, a magnifying glass as small as a square inch in size can collect enough light to start a fire. A little Googling will tell you that the Sun is 400,000 times brighter than the Moon, so all we need is a 400,000-square-inch magnifying glass. Right?

Wrong. Here's the real answer: You can't start a fire with moonlight[1]Pretty sure this is a Bon Jovi song. no matter how big your magnifying glass is. The reason is kind of subtle. It involves a lot of arguments that sound wrong but aren't, and generally takes you down a rabbit hole of optics.

First, here's a general rule of thumb: You can't use lenses and mirrors to make something hotter than the surface of the light source itself. In other words, you can't use sunlight to make something hotter than the surface of the Sun.

There are lots of ways to show why this is true using optics, but a simpler—if perhaps less satisfying—argument comes from thermodynamics:

Lenses and mirrors work for free; they don't take any energy to operate.[2]And, more specifically, everything they do is fully reversible—which means you can add them in without increasing the entropy of the system. If you could use lenses and mirrors to make heat flow from the Sun to a spot on the ground that's hotter than the Sun, you'd be making heat flow from a colder place to a hotter place without expending energy. The second law of thermodynamics says you can't do that. If you could, you could make a perpetual motion machine.

The Sun is about 5,000°C, so our rule says you can't focus sunlight with lenses and mirrors to get something any hotter than 5,000°C. The Moon's sunlit surface is a little over 100°C, so you can't focus moonlight to make something hotter than about 100°C. That's too cold to set most things on fire.

"But wait," you might say. "The Moon's light isn't like the Sun's! The Sun is a blackbody—its light output is related to its high temperature. The Moon shines with reflected sunlight, which has a "temperature" of thousands of degrees—that argument doesn't work!"

It turns out it does work, for reasons we'll get to later. But first, hang on—is that rule even correct for the Sun? Sure, the thermodynamics argument seems hard to argue with,[3]Because it's correct. but to someone with a physics background who's used to thinking of energy flow, it may seem hard to swallow. Why can't you concentrate lots of sunlight onto a point to make it hot? Lenses can concentrate light down to a tiny point, right? Why can't you just concentrate more and more of the Sun's energy down onto the same point? With over 10²⁶ watts available, you should be able to get a point as hot as you want, right?

Except lenses don't concentrate light down onto a point—not unless the light source is also a point. They concentrate light down onto an area—a tiny image of the Sun.[4]Or a big one! This difference turns out to be important. To see why, let's look at an example:

This lens directs all the light from point A to point C. If the lens were to concentrate light from the Sun down to a point, it would need to direct all the light from point B to point C, too:

But now we have a problem. What happens if light goes back from point C toward the lens? Optical systems are reversible, so the light should be able to go back to where it came from—but how does the lens know whether the light came from B or to A?

In general, there's no way to "overlay" light beams on each other, because the whole system has to be reversible. This keeps you from squeezing more light in from a given direction, which puts a limit on how much light you can direct from a source to a target.

Maybe you can't overlay light rays, but can't you, you know, sort of smoosh them closer together, so you can fit more of them side-by-side? Then you could gather lots of smooshed beams and aim them at a target from slightly different angles.

Nope, you can't do this.[5]We already know this, of course, since earlier we said that it would let you violate the second law of thermodynamics.

It turns out that any optical system follows a law called conservation of étendue. This law says that if you have light coming into a system from a bunch of different angles and over a large "input" area, then the input area times the input angle[6]Note to nitpickers: In 3D systems, this is technically the solid angle, the 2D equivalent of the regular angle, but whatever. equals the output area times the output angle. If your light is concentrated to a smaller output area, then it must be "spread out" over a larger output angle.

In other words, you can't smoosh light beams together without also making them less parallel, which means you can't aim them at a faraway spot.

There's another way to think about this property of lenses: They only make light sources take up more of the sky; they can't make the light from any single spot brighter,[7]A popular demonstration of this: Try holding up a magnifying glass to a wall. The magnifying glass collects light from many parts of the wall and sends them to your eye, but it doesn't make the wall look brighter. because it can be shown[8]This is left as an exercise for the reader. that making the light from a given direction brighter would violate the rules of étendue.[9]My résumé says étendue is my forté. In other words, all a lens system can do is make every line of sight end on the surface of a light source, which is equivalent to making the light source surround the target.

If you're "surrounded" by the Sun's surface material, then you're effectively floating within the Sun, and will quickly reach the temperature of your surroundings.[10](Very hot)

If you're surrounded by the bright surface of the Moon, what temperature will you reach? Well, rocks on the Moon's surface are nearly surrounded by the surface of the Moon, and they reach the temperature of the surface of the Moon (since they are the surface of the Moon.) So a lens system focusing moonlight can't really make something hotter than a well-placed rock sitting on the Moon's surface.

Which gives us one last way to prove that you can't start a fire with moonlight: Buzz Aldrin is still alive.

I understand that the New Horizons craft used gravity assist from Jupiter to increase its speed on the way to Pluto. I also understand that by doing this, Jupiter slowed down very slightly. How many flyby runs would it take to stop Jupiter completely?

—Dillon

More than we can afford.

Spacecraft sometimes perform close flybys of heavy, fast-moving planets, which can let them gain speed without using fuel.[1]It may sound strange that you could gain speed by flying toward a planet and then away from it, since intuitively it seems like any speed you gain from flying toward it, you should lose flying away. But it's not really about gravity at all; gravity assists could work just as well with ropes or springs, if you could make them big enough. When you you fly toward a planet, swing around it, and fly back in the direction you came, it's as if you "bounced off" the planet. If the planet is moving, this bounce can give you an extra kick—like a tennis ball thrown at the windshield of a passing truck. You can check out What If #38 for details—or, at least, a drawing of the tennis ball thing. Due to conservation of momentum, the maneuver also slows the planet down very slightly, but no one really worries about that.

Planets don't slow down much during a flyby because they're so much heavier than spacecraft. When New Horizons flew by Jupiter, it gained about 4,000 m/s of velocity, while Jupiter lost about 10^-21 m/s.[2]The geometry is a little complicated, since they were changing both speed and direction. If you want to learn more, look for a copy of this paper; it's a great tutorial.

10^-21 meters per second may not sound like much, but it very slightly changed Jupiter's orbit, shortening its year and bringing it slightly closer to the Sun. Thanks to that flyby, by the time the Sun goes supernova, Jupiter's calendar will be several dozen nanoseconds out of sync from where it would be otherwise!

"Several dozen nanoseconds out of sync" isn't really satisfying, so we'll definitely need more than one flyby. How many can we pull off?

The New Horizons mission cost the US government about \$700,000,000 over the full planned lifetime of the mission from 2001 to 2016. Over that same period, the government spent about \$47,879,840,000,000 on other things. If we cut all the spending on those other things[3]It's probably nothing important. and funneled it all into New Horizons probes, we could have launched 68,000 identical New Horizons probes.

This would create some problems. For one, New Horizons carries a chunk of plutonium for power. This chunk—about 10 kg of it—was made from uranium in a reactor. To make enough plutonium for 68,000 New Horizons would require a substantial chunk of the world's uranium reserves.

But it gets worse.[4]It always seems to, with plutonium. When NASA launches a spacecraft carrying plutonium, they estimate the odds of a launch accident which would release radioactive material into the atmosphere. Usually, these odds are around 1 in 300. With 68,000 launches, then, we can expect a little over 200 nuclear accidents, which probably isn't good.

But it would all be worth it if we could slow down Jupiter! Sadly, 68,000 New Horizons probes aren't nearly enough. We'd still only rob Jupiter of a tiny fraction of its speed. Over the lifetime of the Solar System, the error in Jupiter's calendar would only add up to 2 milliseconds.

If we made the spacecraft cheaper, we could send more of them, but sooner or later we'd start running out of materials. We'd definitely run out of fuel for all these rocket launches, but let's assume we've built some kind of space elevator to make launches cheap. We'd run out of uranium (to make the plutonium) pretty quickly, but we could replace the uranium with a chunk of lead—after all, this spacecraft doesn't really need to work.

Eventually, though, we'd start running out of lead, too. If we replaced the lead with something else—say, rocks, or old garbage—we'd run out of that, too. At some point, in our desperate attempts to reduce Jupiter's forward speed, we'd be reduced to stuffing handfuls of rocks and dirt into a burlap sack with a NASA logo on the side.

Then, believe it or not, we would run out of rocks.

The Earth's crust only has so much stuff[5]This is the technical term. in it. Even if we peeled up the upper few dozen kilometers of crust and flung it at Jupiter—and for the record, I do not recommend we do this—it would trim less than a single mile per hour off Jupiter's speed.

Really, it makes sense that this plan doesn't work. Earth weighs a lot less than Jupiter,[6]Earth weighs almost exactly pi milliJupiters. so even if we throw the entire Earth at Jupiter, it would still only reduce Jupiter's speed by a fraction of a percent—on the order of a few dozen miles per hour. The situation is similar to the one in the tennis ball analogy from earlier: If you want to stop a truck with tennis balls, the tennis balls need more momentum than the truck, which means they need to be extremely heavy, fast, or both.

And at the core, that's the problem with this idea. Gravity assists are just like throwing a tennis ball at a speeding truck, and to stop a truck ...

... you need an awfully big tennis ball.

What would happen if one tried to funnel Niagara Falls through a straw?[1]This question was in reference to this Amazon review of gummy bears—but before you click, be warned that it describes the reviewer's gastrointestinal response to the candy in rather memorable detail.

—David Gwizdala

One would get in trouble with the International Niagara Committee, the International Niagara Board of Control, the International Joint Commission, the International Niagara Board Working Committee, and probably the Great Lakes–St. Lawrence River Adaptive Management Committee.[2]Which is, if I'm understanding these organizational charts right, itself a supergroup made up of three committees for individual bodies of water. Also, the Earth would be destroyed.

Well, that's not quite right. At the risk of stating the obvious, the real answer is, "Niagara Falls wouldn't fit through a straw."

There are limits to how fast you can push fluids through things. If you pump a fluid through a narrow opening, it speeds up. If the fluid is a gas,[3]Gasses are fluids. I know that's weird, but many things are weird. it becomes "choked" when the speed of the gas flowing through the opening reaches the speed of sound. At that point, the gas flowing through the hole can't move any faster—although you can still get more mass to flow through per second by increasing the pressure, which compresses the gas further.

For water, a different effect causes it to choke. When a fluid flows through an opening fast enough, the pressure within the fluid drops due to the Bernoulli principle. Water always "wants" to boil, but is held together by air pressure. Without enough pressure, bubbles of steam form in the water. This is called cavitation.

When the water is forced through an opening at high speed, cavitation bubbles cause it to become less dense overall. Increasing the pressure—to try to push the water through harder—only makes it boil faster. (See page 17 here for a description of this process.)[4]Valve designers try to avoid creating these steam bubbles, because after the bubbles form, they quickly collapse as the pressure rises back up past the valve, and the force from that collapse can gradually eat away at plumbing. This keeps the total amount of water making it through the opening from rising, even if the water-steam mix moves at a higher speed.

Another limit on the water flow rate comes from the speed of sound. You can't use pressure to accelerate water through an opening faster than the speed of sound (in water).[5]It's sort of like a traffic jam—forcing more cars into the back of a traffic jam won't make the ones in the front come out faster. The analogy between traffic jams and choked flows isn't perfect, but I still like it, because it's fun to imagine someone trying to solve traffic jams by using a bulldozer to push more cars into them. However, water very rarely reaches this point, because "the speed of sound in water" is very fast. If you try to make water—which is pretty heavy—go that fast, it tends to start ignoring the turns in your pipes.

So how fast does Niagara Falls need to go to fit through a straw, and is it faster than the speed of sound? This is easy to figure out; all we need to know is the flow rate over the falls and how much area it needs to fit through.

The flow rate over Niagara Falls is at least 100,000 cubic feet per second, which is actually mandated by law. The Niagara river supplies a total of about 292,000 cubic feet per second to the falls, but much of it is diverted into tunnels to generate electric power. However, since people get mad if you turn off the world's most famous waterfall, they're required to leave at least 100,000 of those cubic feet per second flowing over the falls for everyone to look at. (50,000 at night or during the off-season). Sometime in the next few years, the falls may be turned off for maintanence. And probably to see what cool stuff they can find.

(Important note: If you divert the water into a straw, you'll be in violation of the 1950 treaty establishing the "100,000 cubic feet per second" limit. This is monitored by the International Niagara Committee, which consists of one American and one Canadian.[6]Currently, they are Aaron Thompson of Environment Canada and Brigadier General Richard Kaiser of the US Army Corps of Engineers. I'm guessing their enforcement protocol is just some variation on "filing a report," but I like to imagine that they're empowered to physically return the stolen water to the falls by any means necessary. They'll probably be upset with you, as will the other boards I mentioned earlier, so proceed at your own risk.)

A typical straw is about 7mm in diameter. To find out how fast the water flows, we just divide the flow rate by that area. If the result is greater than the speed of sound, our flow will probably be choked, which will lead to problems.

\[ \frac{100,000\text{ }\tfrac{\text{cubic feet}}{\text{second}}}{\pi\left ( \tfrac{7\text{ mm}}{2} \right )^2}=73,600,000\text{ }\tfrac{\text{meters}}{\text{second}}= 0.25c \]

Apparently, our water will be going one-quarter of the speed of light.

On the plus side, we don't need to worry about cavitation, since these water molecules would be going fast enough to cause all kinds of exciting nuclear reactions when they hit the walls of the straw. At those high energies, everything is a plasma anyway, so the concepts of boiling and cavitation don't even apply.

But it gets worse! The recoil from the relativistic water jet would be pretty strong. It wouldn't be enough to push the North American plate south, but it would be enough to destroy whatever device you were using to create the jet.

No machine could actually accelerate that much water to relativistic speeds. Particle accelerators can get things going that fast, but they're typically fed from a small bottle of gas. You can't just plug Niagara Falls into the accelerator input. Or, at least, if you did, the scientists would get awfully mad.

Which is for the best, since the power of the particle jet created by this scenario would be greater than the power of all the sunlight that falls on Earth. Your "waterfall" would have a power output equivalent to that of a small star, and its heat and light would quickly raise the temperature of the planet, boil away the oceans, and render the whole place uninhabitable.

And yet I bet someone would still try to go over it in a barrel.

What percentage of the Sun's heat (per day) does the population of Earth eat in calories per year? What changes could be made to our diets for the amount of calories to equal the energy of the Sun?

—James Mitchell

0.000000000065%.

A McDonald's Big Mac contains 540 (dietary) calories of energy, or about 2,250,000 joules. The Sun's output is 382,800,000,000,000,000,000,000,000 joules per second.[1]Also known as watts. This is a rare case of a common-in-America unit which is secretly SI-friendly. Of course, we immediately worked our way around to measuring stored energy in kWh (and mAh), and now everything is terrible again. That's enough to tell us that we're going to have a hard time catching up with the Sun by eating more burgers.

Why is this so difficult?

Most of the Sun's mass is concentrated in the core, where energy is released as hydrogen fuses into helium. By volume, the Sun's core doesn't actually produce that much energy—a blob of core matter produces about the same amount of energy as the body heat of a reptile of the same size,[2]A Wikipedia factoid also compares the Sun's heat-per-unit-volume to the heat produced by an active compost pile, although the energy production from compost varies with temperature—since a hot compost pile kills off the organisms that do the composting. and less than a warmer-bodied mammal. The Sun is hotter than a reptile^{[citation needed]} because it's so large—all that heat adds up.[3]A large object also has more surface area to radiate heat away, but since surface area is proportional to radius² while the amount of heat-producing material is proportional to radius³, making things bigger generally makes them hotter.

Reptiles may produce heat at approximately the same rate as the stuff in the Sun, but if a reptile doesn't eat for a few weeks or months, it runs out of energy and starves. The Sun, on the other hand, has been burning for billions of years and will last for billions more—because nuclear fusion produces much more energy than metabolizing fat or muscle.

How much more? Strangely, we can come up with a pretty decent estimate just from what we know about animals. Animals live a few weeks—or months, in the case of some snakes—on their own stored reserves, while the Sun will last about 10 billion years. That's a difference of about 100 billion-fold. This is roughly similar to the ratio between the energy stored in a snake-meat Big Mac and the energy stored in a Big Mac-sized chunk of the Sun's core.[5]If you calculate out the exact actual ratios here, you'll find that the sun-to-big-mac energy ratio is a bit lower than the sun-to-lizard lifespan ratio. This is partly explained by the fact that animals are full of bones and brains and stuff, and can't efficiently consume their entire body volume as if they were a giant Big Mac.

If we want to eat enough food to keep up with the Sun's energy-use rate, we have to eat a lot more. A typical person eats a few thousand calories per day, and we probably can't improve on that too much—we can't all be The Rock. To keep up with the Sun, what we really need is more people.

At the end of this article, we imagined a galaxy full of habitable planets, each one hosting 7 billion clones of former solicitor general Ted Olson. (Don't ask.) If the Teds ate a normal diet, the total calorie consumption of that galaxy would still fall short of the Sun. We'd need approximately a thousand galaxies worth of burger-eating Ted Olsons to achieve our goal.

It's important to spread this food consumption out across multiple galaxies, because if you gathered all that food in once place, you'd have a big problem. Since food has such a low energy density compared to the Sun, you need a lot of food to keep up with the Sun. Matching a few days' worth of Sun output would require a sphere of hamburgers the size of the Earth, and keeping up with the Sun over its entire lifetime would take a pile of burgers much larger than the Sun. In fact, it would be heavier than the supermassive black hole at the center of the galaxy.[6]Which would promptly create a new black hole. And possibly a new center of the galaxy, for all I know, although I'd want to play with Universe Sandbox for a while before making any sort of guess about how that would play out.

The bottom line: If you want to keep up with the Sun's output by feeding people burgers, you'll need to open some intergalactic franchises.

My boyfriend recently took a flight on a plane with wifi, and while he was up there, wistfully asked if I could send him a pizza. I jokingly sent him a photo of a parrot holding a pizza slice in its beak. Obviously, my boyfriend had to go without pizza until he landed at JFK. But this raised the question: could a bird deliver a standard 20" New York-style cheese pizza in a box? And if so, what kind of bird would it take?

—Tina Nguyen

A bird could, possibly, deliver a pizza to a house. Delivering it to an airliner is a lot harder.

A 20-inch pizza weighs about 1.8 kg.[1]Citation: I just ordered a pizza to check. I usually steer clear of experimental science in these articles, but am willing to make an exception when it involves eating a bunch of pizza. That's about 100 times the weight of a sparrow, so we're definitely going to need a large bird. There are all sorts of birds bigger than our pizza, including eagles, swans, cranes, pelicans, and albatrosses. However, some of them would do better at pizza delivery than others. To see why, let's take a look at wing shapes.

Birds have different types of wings depending on what kind of flying they need to do. Of all the types of wings, the ones best suited for pizza delivery are probably the relatively short-and-broad kind found on many soaring hawks and eagles.[2]Long, thin wings, like those of a gull or albatross, are more aerodynamically efficient in many ways. However, these wings are harder to flap, which makes it difficult for these birds to accelerate quickly. Albatrosses require long "runways" to build up speed before they can lift off.​[3]Here's a live feed of some baby albatrosses nesting in Hawaii. These wings are good for taking off while carrying a heavy load, which is of course necessary for pizza delivery.

The largest birds of prey in North America[4]Not counting the California condor, which isn't very good at the kind of hard flapping required to lift heavy loads. And anyway, there are only a few hundred of them in the world—up from 22 in the early 1990's—so someone would definitely notice if you took some for pizza delivery. are the bald eagles[5]Here's a live feed of a bald eagle nest in the US National Arboretum. and golden eagles, which weigh about 4 or 5 kilograms when fully grown. The famous viral video of a golden eagle snatching a toddler is fake, but eagles have been seen to lift some awfully heavy things. Last year, photographer Alex Lamine saw a bald eagle in Georgia carrying a 12-pound (5.4 kg) tree branch, presumably to add to its gigantic nest. The eagle dropped the branch before making it back to the nest, but it definitely proved the bird was capable of flying—at least briefly—while carrying a load equal to its own body weight.

As a general rule, though, birds of prey won't try to pick up more than about half of their own weight. This means a half-kilogram peregrine falcon[6]Here's a live feed of a peregrine falcon nest box in Arizona. couldn't pick up our 2-kilogram pizza. A 5-kilogram eagle, on the other hand, probably could.

However, picking up a pizza is one thing, but what about delivering it to an airliner?

Soaring birds like vultures—and eagles—can ride thermals[7]Thermals, warm columns of rising air, are a phenomenon familiar to both glider pilots and fans of the Animorphs book series. to extreme heights. In tropical regions, where the sunlight-powered thermals are strongest, planes have encountered[8]😞 soaring Rüppell's vultures at altitudes of over 10 kilometers. That's high enough to reach a cruising airliner—but, unfortunately, this kind of soaring flight requires ideal flying conditions. "Having a pizza strapped to you" is definitely not that.

So a bird could potentially carry a pizza, but it couldn't fly up to an airliner with it. That's just as well, because there's one more major problem you'd face: Speed.

Whether or not a bird can fly as high as an airliner, it definitely can't fly as fast. Even if the person in the plane managed to get the emergency door open, they'd have to find a way to grab the pizza.

If you tip a pizza box too far, the cheese runs off one side. This critical angle varies from pizza to pizza and depends greatly on temperature, but let's suppose it's about 45°. That angle tells us that a pizza can handle a maximum sideways acceleration of about 1g.[9]Assuming you've managed to keep the pizza warm at those high altitudes—because what kind of a monster delivers a cold pizza? To accelerate up to an airliner cruising speed of 500 mph, we'll need the acceleration to happen over a distance of over a mile. In other words, we'd need a mile-long mechanism trailing behind the plane to gently reel in the pizza.

But wait—those calculations assume sideways acceleration. Pizzas—like humans—handle "face-first" acceleration best. If the pizza were rotated during the handoff, it could survive a much greater acceleration, allowing the grabbing mechanism to be smaller.

What kind of face-first acceleration can a pizza survive before it spreads out to fill the bottom of the box? I haven't found any data on that, but if anyone wants to try to sneak a pizza into a centrifuge, go for it. Be sure to take pictures!

All in all, if you're in a plane and feel the urge to order a pizza, it's probably easier to just wait until you land. Then, if you really want, you can try to get a bird to deliver it.

But don't be surprised if some slices go missing along the way.

Since rainbows are caused by the refraction of the sunlight by tiny droplets of rainwater, what would rainbow look like on Earth if we had two suns like Tatooine?

—Raga

A planet with double suns would have double rainbows.

Or rather, quadruple rainbows. Our rainbows here on Earth are already double rainbows—there's a second, fainter bow above the main one. You can't always see this second rainbow, since the clouds need to be just right, so people get excited when they see one.

The area between the two rainbows is darker than the area outside because raindrops reflect light more strongly in certain directions. That region has a name, by the way—it's called Alexander's dark band.

The first and second rainbows are the only ones you can see easily, but there are actually many more bows beyond those two, each one fainter than the last. Rainbows are formed by light bouncing around in raindrops, and the different bows are formed by different paths the light can take. The main rainbow is formed by the most common paths through the droplet, and other paths—where some of the light bounces around in more unusual ways—make the fainter second, third, fourth, and even fifth rainbows.

Usually, only the first and second rainbows are bright enough to see; it was only in the last five years that anyone took pictures of the third, fourth, and fifth rainbows.

Rainbows appear on the other side of the sky from the Sun, so to figure out what a double rainbow would look like on a planet with two suns, we need to figure out where the suns usually appear in the sky on that kind of planet.

There are planets with two suns out there, although we didn't know that for sure until recently. Double-star planets come in two main varieties:

In the first kind of system, the two stars are close together and the planet goes around them far away. This kind of planet is called a circumbinary planet. In the second kind of system, the two stars are farther apart, and the planet orbits one of them[1]Not necessarily the bigger one. while the other stays far away. This kind of planet is called [the other kind of planet].[2]I'm sorry, I've just never learned a good word for these.

If you lived on [the other kind of planet],[3]Sorry. the two Suns would spend most of the year in different parts of the sky. Depending on how big they were, they may also be very different in brightness. If you were orbiting the larger star, the smaller one might be no brighter than the Moon,[4]Which would still be bright enough to cast a rainbow! or even look like an ordinary planet or star.

Tatooine, in Star Wars, looks like it's probably a circumbinary planet. The two stars appear pretty close together in the sky and similar in color and size, so it seems reasonable to guess they're actually near one another, with Tatooine orbiting both of them. Two suns would create two overlapping rainbows. The main bow of the rainbow is a circle about 84 degrees across, centered in the sky exactly opposite the Sun.[5]This is why you never see more than half of a rainbow above the horizon. If the center of the rainbow were above the horizon, it would mean the Sun was below it behind you, so there wouldn't be sunlight to make a rainbow in the first place. The farther apart the two suns were, the farther apart the rainbows would be. If the two suns were 84 degrees apart, the main bows of the two rainbows would barely touch.

A pair of suns 84 degrees apart would be possible around [the other kind of planet], but not around Tatooine-type[6]If Star Wars had just used the other kind of planet, we could use its name for them and solve this problem. circumbinary planets. The reason is simple: A planet orbiting two stars can't get too close to them or its orbit becomes unstable. If it gets too close, the irregular tugging from the gravity of the two stars as they orbit will eventually cause the planet to crash into one of them or get flung out of the system.

For a system with two similar-sized stars, this "critical radius" is around six times the distance between the two stars.[7]This is a very rough number; it can range from four to eight depending on the exact arrangement. We've found a lot of planets close to that critical radius, which suggests that maybe they slowly migrate inward until they reach it and are ejected or destroyed. Strangely, we haven't found many big Jupiter-sized planets around binary stars in general; we should be seeing them if they're there, so the lack of them is a mystery. This means that the two suns would never get more than about 20 degrees apart in the sky:

This tells us that the two rainbows in a Tatooine-like system would always overlap.[8]Assuming the raindrops are made of water, or something with similar refractive properties. The colors would blend together where the bows crossed, and the dark bands would too.

I suppose doubling all the rainbows would also double the number of pots of gold at the end of each rainbow.[9]Come to think of it, do our rainbows have one pot of gold or two? I've never really thought about it. And it's not just pots of gold; I guess we'd need to rethink all kinds of rainbow references.

Overlapping rainbows would be beautiful, but definitely a lot more complicated.

How many fireflies would it take to match the brightness of the Sun?

Luke Doty

Not that many! I mean, it's definitely one of those gigantic numbers with lots of zeroes, but in the grand scheme of things, there aren't as many zeroes as you might expect.

Our first question: Where does firefly light even come from?

Fireflies may look like they're full of glow-in-the-dark goo, but the light they give off actually comes from a thin layer on their surface.[1]You can see some diagrams of the organs here and here. Lots of insects have glowing surface patches, and some of those patches have been studied carefully to calculate their brightness. A 1928 paper on beetles called "headlight bugs"[2]Such a great name. found that their glowing patches, which were a little over a square millimeter in area, emitted about 0.0006 lumens of light. Fireflies have luminous organs (bright patches) that are about the same size as those of headlight bugs,[3]See this paper on some common American fireflies. and their organs tend to have a similar peak brightness per area, so this figure is a good guess for the brightness of a firefly's lantern.

Firefly lights aren't "always-on." They blink on and off, with patterns that vary from species to species and situation to situation. These flashes carry information, some of which you can decode using this delightful chart.[4]You can also use LEDs to mess with firefly patterns, which feels strangely invasive.

To get the brightest light, let's assume we're using a species with a mostly-on duty cycle—like a headlight bug. How does its 0.0006-lumen light output compare to the Sun?

The Sun's brightness is \( 3.8\times10^{28} \) lumens, so by simple division, it would take \( 3\times10^{31} \) of those fireflies to emit the same amount of light. That's a surprisingly small number; adult fireflies weigh about 20 milligrams, which means \( 3\times10^{31} \) fireflies would only weigh about a third as much as Jupiter and 1/3000th as much as the Sun.

In other words, per pound, fireflies are brighter than the Sun. Even though bioluminescence is millions of times less efficient than the Sun's fusion-powered glow, the Sun can't afford to be as bright because it has to last billions of times longer.[5]If you like Fermi problems—and silly equations—there's an interesting route you can take to this answer without doing any research on fireflies or the Sun at all. Instead, you can just plug this equation into Wolfram|Alpha: (5 billion years / (4 hours/day * 3 months)) / (1% * (speed of light)^2 / (3200 calories/pound)).

Let's walk through it: The first half—the numerator—is a guess for the ratio between how long the Sun has to keep glowing compared to how long a firefly does. I took a wild guess that fireflies have to light up for a few hours each night for one summer, while the Sun has to last another five billion years. The second half—the denominator—is a guess as to the ratio between the stored energy in a pound of firefly vs a pound of star. Nuclear fusion converts about 1% of the input matter to energy, so from E=mc², the stored energy is c² kg/kg, whereas animal matter (say, butter) is about 3,200 food calories per pound. The result should tell us the ratio between a firefly's brightness per pound and the Sun's. And the answer we get says that the fireflies are a few thousand times brighter—which is roughly what we got from working through it the other way!

It's true that we got lucky with some of our guesses, but since we made errors in both directions, they tended to cancel out. This kind of thing works more often than it seems like it should!

But wait! A mass of fireflies that big would run into problems. Besides the obviousproblems with gathering that many animals in one place, the fireflies would block each others' light. The inner fireflies would be hidden behind the outer ones, and the total brightness would be limited.[6]But the light from the core fireflies wouldn't just vanish. After bouncing around a few times, it would be absorbed by neighboring fireflies, which would get warmer. This is sort of like how radiation makes its way out of the Sun's core—but in the case of the fireflies, they'd die from the heat before the process got very far.

Since the only light that matters is the light at the surface, we could imagine arranging the fireflies in a hollow sphere, with their lanterns pointing outward. Or, to make thing simpler, we could imagine a single giant firefly. How big would it need to be?

Since we know our firefly will need to give off about \( 3\times10^{31} \) times as much light as a normal firefly, it will need a glowing patch \( 3\times10^{31} \) times larger. Since surface area is proportional to length squared, our firefly will have a body length \( \sqrt{3\times10^{31}}=5\times10^{15} \) times longer than a normal firefly, which would make it about the size of the Solar System.

Since mass is proportional to length cubed, our firefly would weigh \( \left( 3\times10^{31}\right)^{\tfrac{3}{2}}=1.6\times10^{47} \) times as much as a normal firefly, which works out to about half as much as the entire Milky Way galaxy.

Such a firefly would immediately collapse under its own weight and become a black hole. In fact, given the distribution of galaxies in our universe, there's an upper limit to how large black holes can grow, and this firefly would be bigger than that limit. That means our firefly would become the largest black hole in the universe. It would give off a lot of light as it devoured our galaxy, and then, eventually, it would give off none at all.

Black holes last a long time, but they eventually evaporate through Hawking radiation. When the black hole era of our universe comes to an end, black holes will evaporate one by one, with the smallest evaporating faster. Since our firefly's black hole would be the largest one in the universe, it would be the last to evaporate—a final outpost of irregularity in a universe fading toward heat death.

We should probably add that to the identification chart, just in case.

Since Death Valley is below sea level could we dig a hole to the ocean and fill it up with water?

—Nick Traeden

Yes! We can do anything we want. We shouldn't do this, though, because it would be gross.

Death Valley is an endorheic basin[1]"Big hole" in California. The floor of the valley is about 80 meters below sea level. It contains the lowest point on land in North America[2]Excluding artificial points like mines. and is the hottest place on Earth.[3]If you're about to say "Wait, what about Liby—," then don't worry, I'm with you. Just hang on and read a few more words ahead!

Now, if you're the sort of person who's into world records, you might have heard that the hottest place on Earth was Al Azizia, Libya. Al Azizia recorded a temperature of 58.0°C (136.4°F) in 1922, a mark Death Valley has never come close to. So what gives?

It turns out Al Azizia has recently been stripped of its record. In 2010, an exhaustive—and definitely a little obsessive—investigation led by Christopher C. Burt convinced the World Meteorological Organization that the Libyan measurement was probably a mistake. This left Death Valley with the record of 56.7°C (134°F), set in 1913. Case closed!

Except it's not quite settled. Burt has raised questions about the 1913 record as well, and has gone so far as to catalog a number of historical extremes along with a credibility score for each. The "real" record is probably 53.9°C (129°F). This temperature has been recorded four times, in 1960, 1998, 2005, and 2007—every time in Death Valley.

These records were recorded with modern instruments and are considered reliable. They also make sense from a theoretical point of view. Geographers have calculated[4]This Army Corps of Engineers publication cites a couple of sources for this, including a 1963 paper by G. Hoffman. Unfortunately, that paper is in German, which I can't read, so I've just decided to trust that the Army Corps of Engineers writers Dr. Paul F. Krause and Kathleen L. Flood aren't pulling a fast one on me. that the highest possible temperature in ideal spots (in desert basins like Death Valley) during the 20th century is 55°-56°C, so 54°C sounds like a reasonable world record.

Now, back to Nick's question.[5]This is nowhere NEAR the record for "most boring digression into world record trivia." That record was recently challenged by IBM computer capable of producing millions of boring pieces of trivia per second, but the machine narrowly lost to reigning human champion Ken Jennings.

Since Death Valley is below sea level, we could, as Nick suggests, flood it with seawater. It would take a lot of digging, since there's a lot of Earth in the way. The lowest route to Death Valley is probably by traveling up the Colorado River watershed, along the Arizona border past Quartzsite,[6]Trivia: If you want to reach Quartzsite, Arizona from my school, Christopher Newport University, you just step out onto Warwick Blvd (Rt. 60) and turn left. That's it—Route 60 runs across the country, from the CNU campus in Virginia to I-10 just outside Quartzsite. then northwest[7]Possibly following one of the routes shown on page G34 in this report. past Zzyzx, which is a real place.

If you did all that digging, you could create a channel from the Gulf of California to Death Valley, and water would flow in. We can use this handy stream-flow calculator to figure out how wide we'd need to make the channel. A channel 20 meters deep and 100 meters wide should be able to fill it in a few months. A really wide channel—like the kind carved by glacial floods—could fill it in hours.

We know it's possible to create this kind of inland sea because we've done it before—by accident. In 1905, irrigation engineers working on the Colorado River made some mistakes. During a flood, the entire Colorado river broke through into the Alamo Canal and flowed directly into the Salton basin to the north. By the time they repaired the canal, two years later, the Salton basin had become the Salton Sea—one of the larger human-caused changes to the world map.

The Salton Sea is fed mainly by agricultural runoff, so it's become saline[8]"Salty" and hypereutrophic.[9]"Gross" Large numbers of dead fish, combined with algal decay and unusual chemistry, have created a smell that the US Geological Survey describes as "objectionable," "noxious," "unique," and "pervasive." The sea is a birdwatching hot spot, but also the site of a lot of mass bird die-offs, so kind of a mixed bag if you're into birds. In recent years, the water has been evaporating quickly, leaving behind dried toxic residue which is swept up into dust storms. Work to clean up and rehabilitate the region is ongoing.

All in all, the Salton Sea is a mess—and Nick wants to make another one.

Nick's Death Valley project would start off connected to the ocean, but without a source of flowing water at the Death Valley end,[10](It's a desert.) the channel would gradually silt up. The link to the ocean would eventually be broken, the sea would start to evaporate, the water would become saline, algae would bloom, and eventually the US Geological Survey would start complaining about the smell.

There would be one more consequence to all this. Thanks to the flood of cold ocean water burying the whole region, Death Valley would stop setting temperature records, and someone else would eventually claim to have broken their 129°F record. The Death Valley records would have to be compared to the newer candidates, which would probably use slightly different methods ... and that means one thing:

A World Meteorological Organization expert panel!

What is the longest English word you can spell using the one letter abbreviations of the 20 genetic amino acids? What about the three letter abbreviations? What would the resultant peptides look like?

—Kira (Lysine-Isoleucine-Arginine-Alanine) Guth

These are the 20 amino acids that appear in our genetic code:

Since the 20 amino acid abbreviations include most of the common letters, you can spell almost anything you want with them.

There are lots of novelty "longest words" in English. Since there's no standard English dictionary, the actual longest word is just a question of what we're willing to let someone get away with. We all like Julie Andrews, so we usually allow "supercalifragilisticexpialidocious."[1]Holy crap, I spelled that right on my first try. Many people have memorized other novelty words like "antidisestablishmentarianism."

The longest words that a regular English speaker might hear or use in casual conversation is probably uncharacteristically (20 letters),[2]Tied with compartmentalization, indistinguishability, and internationalization. and the longest "normal" word without getting too cute about prefixes[3](and sounding precocious) might be deinsitutionalization (22 letters).[4]Tied with counterrevolutionaries and electroencephalography. overintellectualization is arguable at 23.

None of those 20-plus-letter words can be spelled with the 20 allowed amino acid letters. The longest reasonably common word that can be spelled with those letters is probably interdepartmentally (19 letters), although it again comes down to what you consider "common".

How about the three-letter abbreviations?

The three-letter amino acid abbreviations turn out to be surprisingly tough to make words from. A few of them are words themselves (like his), but there's only one word that can be made by combining them: SER•VAL (SV, serine-valine), a type of cat native to Africa.

What would these peptides look like?

Well, that's hard to answer without synthesizing them. The peptide INTERDEPARTMENTALLY is long enough that it almost certainly doesn't appear in any existing genetic sequence, and SV (serval) is short enough that it's common everywhere and doesn't really mean much on its own.

But what's the longest word that does appear in a known peptide/protein[5]A peptide is a short sequence of amino acids, while proteins are longer sequences made up of peptides, but the line between them is pretty arbitrary. sequence?

There are some tools for searching known proteins, including PepBank, UniProt, and PeptideDB. By downloading and searching through some of these peptide databases, we can look for English words spelled out using amino acid abbreviations.

It's easy to find four- or five-letter words in these peptide sequences, and you can come across a few seven-letter ones here and there. One random peptide sequence from the 11th chromosome of the human genome, MADSVKTFLQDLARMLESSKRERSSVEEGQVVSWHREEPRV, contains the seven-letter word armless (UniProt entry).

You also, occasionally, come across eight-letter words:

• GRISETTE, a type of mushroom, which appears in a brain-related NXPE family member 3 precursor[6]Don't ask me. protein.

• DATELESS, which appears in a protein involved in controlling cell growth which may be important in cancer.

• REVERSAL, which appears in the sequence on chromosome 1 which encodes the protein rootletin. Rootletin is a fibrous protein found in the base of cilia, the little hairlike fibers that stick out of our cells. These fibers (also called flagella when there are few of them) are sometimes used to push things around; cilia in our lungs help push out dirt and debris. These gadgets can also enable individual cells to swim; this is how sperm cells and ulcer-causing bacteria push themselves around.

The universe of proteins is enormous, and there are certainly longer words lurking out there somewhere, waiting to be found. If you find a peptide containing a longer word, you could be eligible for a Nobel Prize—but only in the sense that anyone who's not dead is technically eligible.

Lastly, let's return to Kira's question. In her email, Kira gave her name as Lysine-Isoleucine-Arginine-Alanine, or KIRA. I searched for this sequence in a few peptide databases, and I have some good news, some bad news, and some gross news.

The gross news is how the sequence was found. Strep throat, and many common skin infections, are caused by Streptococcus bacteria. In 1995, researchers isolated several proteins produced during these infections, looking for possible targets for antibodies. One of the proteins they found was WYSLNGKIRAVDVPK, or GKIRAV for short.

The bad news is that the researchers filed a patent which includes this sequence. The patent, published in 1999, gives the researchers exclusive control over this protein. If Kira wants to mess around with the protein, she could—in theory—be sued.

The good news is that in 2013, the Supreme Court struck down this type of gene patent. The case, Association for Molecular Pathology v. Myriad Genetics, Inc., involved the patents protecting tests for genetic cancer risk. That means Kira is totally free to produce as much WYSLNGKIRAVDVPK as she wants.

But I would still advise against it.

What if the entire continental US was on a decreasing slope from West to East. How steep would the slope have to be to sustain the momentum needed to ride a bicycle the entire distance without pedaling?

—Brandon Rooks

Too steep to actually build, sadly. But for the next best thing, I suggest a vacation to the Hawaiian island of Maui.

First, the physics. Bikes coast downhill. On a long enough slope, a bike will reach a certain steady coasting speed. On a steep hill, their coasting speed will be faster, and on a gentle slope, they coast more slowly. If the slope is small enough, the bike will slow down and stop.

The shallowest slope at which a bike will still roll steadily forward is determined by the bike's coefficient of rolling resistance. In fact, the formula for this minimum slope—measured in terms of vertical drop over horizontal distance—is incredibly simple:

\[ \text{Minimum slope} = \text{Coefficient of rolling resistance} \]

"Slope equals coefficient of friction"[1]Sliding friction and rolling resistance work in different ways, but the coefficients are equivalent in these types of problems. If you want to be precise, you could use the phrase "coefficient of resistance" for all of them, but "coefficient of friction" is the more common term. is a handy general rule in physics: The coefficient of friction between an object on a surface is just the shallowest slope at which the object slides.[2]The coefficient of static friction is the slope at which the object starts sliding. The (usually lower) coefficient of dynamic friction is the minimum slope at which it keeps sliding once you give it a nudge.

For a nice bike under good conditions, the coefficient of rolling resistance can get as low as 0.002, or 1/500.[3]You can browse some test data here. That means that to travel 500 miles horizontally, you'll need a vertical drop of at least 1 mile. To travel the roughly 2,500 miles from New York to LA, you'd need to start off at least 5 miles up, higher than North America's highest mountain. I suggest bringing oxygen tanks.

But be warned—the trip could take a while.

A bike's rolling resistance mainly comes from the way the tire[4]And the ground, if you're riding on dirt.​[5]And the spokes and frame, if your bike is made of soft clay or something.​[6]Why do you have a bike made entirely of soft clay? deforms as it rolls, and it doesn't depend that much on how fast you're going. Air resistance, on the other hand, increases as you speed up, and under most conditions is the main drag force acting on a moving bike. To figure out how fast a bike will coast on a downhill slope, you need to calculate the point at which air resistance balances out the forward pull from gravity. At that point, the bike will stop accelerating. We can do that by using the formula for air resistance:

\[ \text{Forward pull from gravity} = \text{Rolling resistance} + \text{Drag force} \]

\[ m g \sin(\theta) = g \cos(\theta) C_r m + \tfrac{1}{2} C_d \rho A V^2 \]

\[ V = \sqrt{\frac{m g \sin(\theta) - g \cos(\theta) C_r m}{ \tfrac{1}{2} C_d \rho A}} \]

(V is the speed of the bike, C_r and C_d are the coefficients of rolling resistance and air drag, θ is the slope angle, g is the acceleration of gravity, m is the mass of the bike and rider, A is the frontal area of the bike and rider, and ρ is the density of air.)

For a very shallow slope of 0.2° or 0.3°, the bike would barely roll, and its top speed would be slower than a walking pace. You would need to add an extra few tenths of a degree to get the speed high enough to balance comfortably, and this would make the LA end of the slope even higher than the already implausible five miles.

But still, bicycles are pretty impressive coasting machines.[7]Trains have steel wheels which roll on smooth rails, so they should have very little rolling resistance. You can work out their coefficients by looking over technical specs or calculating from first principles, but a cleverer way is by watching train-pulling athletic events. Then, with a little calculation involving the limits of human strength and/or direct measurement, you can work out the coefficient from the other end. It turns out that train cars—at least, the kind used in strongman events—have coefficients of rolling resistance barely equal to that of a good bicycle. Skis, which are pretty good at sliding, actually have a coefficient of friction about 10 times higher than a bike's rolling resistance.

To ski from LA to New York, a skier would need to start off 10 times higher than a bike to make the same trip. Instead of the top of a mountain, they would need to start from near the edge of space. Not only is there no way to build a slope that tall, but ice isn't even stable at those low temperatures, so there'd be nothing to slide on.

In practice, the longest horizontal distance you could travel on a bike with an ideal ramp is probably not more than a couple hundred miles, and that would require ideal conditions. In the real world, the longest such trip might[8]It's billed as the longest, but I wonder if there's a longer one in some random stretch of gently-sloping downhill road in rural Mongolia or something. be the Haleakala downhill bike ride, which allows you to take a 35-mile trip from near the 10,000-foot summit all the way down to sea level with virtually no pedaling required.

(And if you can't make it to Maui yourself, you can at least enjoy the video search results for bicycle into water.)

Would a toaster still work in a freezer?

—My Brother, My Brother and Me, Episode 343, discussing a Yahoo Answers question

On a recent episode of Justin, Travis, and Griffin McElroy's terrific advice podcast, My Brother, My Brother and Me, the brothers pondered a Yahoo Answers question about what would happen if you put a toaster inside a freezer. (The discussion comes around the 36-minute mark.)

They have a fun discussion of a few aspects of the problem before eventually moving on to the next question. Since they don't really settle on a final answer, I thought we could help them out by taking a closer look at the physics of freezer toasters.

(A quick safety note: If you actually do this, keep in mind that the toaster may melt some of the ice in the freezer, leaving you with a running electrical appliance in a pool of water.)

Griffin sums up the situation like this:

You put a toaster in a freezer. You run the extension cord in there. You put some good bread in there. You click it down. What even happens, right? Because if your answer is, "it would get hot," then the freezer hasn't done its job. But if you say "it would get cold," then the toaster hasn't done its job.

For starters, the answer: The toaster would win. The freezer wouldn't do its job. Toasters beat freezers.

It's easy to think of a toaster and freezer as equivalent—one cools things down and the other warms them up. But toasters heat things up a lot more than freezers cool them down.

The coils in regular toasters get hot enough to glow, which means they're over about 600°C. Since the toaster is operating at such high temperatures, it would hardly notice whether the surrounding environment is 20°C (room temperature), 4°C (a fridge), or -15°C (a freezer).[1]The zero on our usual temperature scales can confuse things, since it makes it seem like going from 10° to 20° is "doubling" the temperature. But the "zero" on the Celsius scale is just a point chosen by convention. If we switch to Kelvin, which counts in degrees above absolute zero, a freezer is 260 K, a fridge is 275 K, a normal room is 295 K ... and the heating element in a toaster is 900 K.

The toaster needs to heat its coils from room temperature to somewhere over 600°C. From the toaster's point of view, a 20- or 40-degree change in starting temperature hardly matters. The coils will get hot, and then the bread will get hot, too. If the bread is colder at the start, the toaster will have to heat it a little longer to get it up to ideal toasting temperature, but it will have no trouble getting there. As anyone who's ever burned a piece of toast knows, toasters are definitely capable of heating bread to above the ideal temperature for toast.

In their discussion, the McElroys brought up another question: Even if the toaster can still toast bread at first, would it struggle to stay warm over time? If you left both the toaster and the freezer running, who would win in the long term?

The answer is that the toaster would still win. A toaster produces about a thousand watts of heat, and the cooling system in a household freezer can't remove heat that fast. In fact, since freezers are so well insulated, the inside of the freezer would probably get much hotter than the rest of the house, and eventually the toaster and/or the freezer would probably overheat.[2]Either device have a safety cutoff that stops things from actually melting down, but it's probably not wise to count on that in this situation.

Refrigerators and freezers work by soaking up heat from their interior and dumping it out the back.[3]That's why the area behind your freezer is warm, and why you can't cool a room by leaving the fridge door open. In a sense, they're more efficient than toasters. Fridges have a "coefficient of performance" of 2 or 3, which means it only takes them 1 unit of electrical energy to move 2 or 3 units of heat energy from the interior to the exterior. A toaster, on the other hand, produces 1 unit of heat from 1 unit of electricity. But since the compressor in a fridge-freezer typically only uses 100 or 150 watts when it's running,[4]You can see some real-world graphs of refrigerator power usage, courtesy people with home electricity meters, with a simple Google Image search. The distinctive on-off square-wave pattern is the compressor switching on and off throughout the day, while the big spikes are the heating element that keeps frost from building up on the coils. This power consumption is split between the fridge and the freezer, but if the fridge is already cold, most of the energy will be spent fighting with the toaster. so even with the efficiency multiplier, it can't keep up with the toaster's 1000+ watts of heat production.

Eventually, the toaster will start to heat up the inside of the freezer. Even if the freezer were as powerful as the toaster, it wouldn't be able to keep the toaster coils themselves from getting hot and toasting bread. The freezer can make the air around the toaster cold, but remember, to the toaster, all our air is cold.

If you happen to live in the Canadian city of Winnipeg, you can check this experimentally. The winter temperature at night in Winnipeg is about the same as the inside of a freezer, so the environment there effectively simulates a freezer with infinite capacity to absorb heat. Suppose you put a toaster out on your porch one night, plugged in by an extension cord, and leave it running for a few hours, going outside every so often to collect the toast and put in some fresh bread. What will happen? Simple: You'll quickly be eaten by wolves.

But assuming you survive the experiment, you should find that the toaster doesn't have trouble working in the cold air. It may take a bit longer to get the bread properly browned, but unless the wind is extremely strong, it should be able to manage it fine. After all, to a toaster, all weather is cold.

The difference between what humans consider "cold" and "warm" is negligible in a lot of high-temperature processes. For example, Antarctica has a well-equipped fire department. It might seem strange to worry about things getting too hot in the coldest place on Earth, but fire poses a serious threat to the researchers there. After all, the place is dry, windy, and doesn't have a lot of liquid water sitting around to douse a flame with. Sure, it's cold—but to a fire, everything is cold.

On the other hand, there are no wolves in Antarctica. So as long as you don't mind a trip—and you get clearance from the Antarctica fire department—you can go there to enjoy your outdoor freezer toast in peace.

I used to work on a fisheries crew where we would use an electro-fisher backpack to momentarily stun small fish (30 - 100 mm length) so we could scoop them up with nets to identify and measure them. The larger fish tended to be stunned for slightly longer because of their larger surface area but I don't imagine this relationship would be maintained for very large animals. Could you electrofish for a blue whale? At what voltage would you have have to set the e-fisher?

—Madeline Cooper

So you want to give endangered whales powerful electric shocks. Great! I'm happy to help. This is definitely a very normal thing to want to do.

There are various electrofishing setups, but they all operate on the same general principle: An electric current flows through the water, and also through any fish that happen to be in the water. The electric current, through a few different physical effects, draws the fish toward one of the electrodes and/or stuns them.

For a long time, people didn't really notice that electrofishing injured fish at all. For the most part, stunned fish seemed to be fine after a few minutes. However, they frequently suffer from internal damage which isn't obvious from the outside. The electric current causes involuntary muscle spasms, which can fracture the fish's vertebrae. As this paper shows, these kinds of spinal injuries are more common and severe in larger fish.

As you mention, for a given electrofishing setup, larger fish are usually more affected than smaller ones.[1]This can lead to larger fish being overrepresented in sampling studies. Why? Well, we don't know. In their comprehensive 2003 study Immobilization Thresholds of Electrofishing Relative to Fish Size, biologists Chad Dolan and Steve Miranda modeled the way electric currents stun fish of different sizes, but caution that "no adequate conceptual system exists to explain the effects of size on electroshock thresholds from the perspective of electric fields."

None of these studies dealt with animals anywhere near the size of whales. The largest fish in Dolan and Miranda's study were still quite small. This experiment tested larger fish up to 80cm long,[2]The fish they used in the experiment grew rapidly to a range of sizes, mainly because the larger ones kept eating their smaller siblings. but nothing whale-sized.[3]There's been at least one case of dolphin death linked to illegal electrofishing. Since we don't know exactly why larger fish respond differently, it's hard to confidently extrapolate.

Fish are typically[4]Actual quote from that paper: "The results for these tests were unsettling ... this observation was so unexpected that we stopped the experiment to recalibrate the equipment." stunned by equipment delivering about 100 µW of power per cm³ of body volume, so for a whale, that would be about 20 megawatts.

But there's a catch: Most electrofishing is done in fresh water. Unfortunately, blue whales live in the ocean,[5]I mean, unfortunately for Madeline. It's fortunate for the whales. where the salt water conducts electricity much more easily. That might seem like good news for our electrofishing plans, but it turns out to make it much more challenging.

Electrofishing works best when the water and the target animals are about equally conductive. In highly conductive saltwater, most of the current flows past the animals in the water rather than through them. This means that ocean electrofishing requires much more power. Using our simple extrapolation, instead of 20 megawatts, we might need a gigawatt. In other words, you'll need to bring a large nuclear generating station.

Simple extrapolation is misleading here, since we know that large animals respond to electricity differently. How differently? Well, according to an electrofishing.net post by Jan Dean, a human who fell into the water in front of a typical electrofishing boat could easily die.[6]While it sounds dangerous, people aren't often killed during electrofishing accidents. The 2000 EPA report "New Perspectives in Electrofishing" comments that "In the United States, since World War II, only about five electrocutions during electrofishing have been documented." I assume they just mean records weren't kept before World War II, but it's technically possible that the war involved so many electrofishing deaths that they need to exclude it from the stats. Blue whales, which are even larger than humans,^{[citation needed]} would presumably fare even worse.

Electrofishing temporarily stops a fish's heart.[7]Until reading this paper, I didn't know clove oil was used as a fish anesthetic. You learn something new every day! The fish seem to recover, most of the time, but humans—and probably whales—have a harder time with cardiac arrest.

It's possible that giving blue whales massive electrical shocks isn't as good an idea as it sounded at first.

That's not to say there's no place in science for giving random electric shocks to large aquatic animals. A project at the Denver Wildlife Research Center used electrofishing-style equipment—linked to an infrared camera—to repel beavers, ducks, and geese from selected areas. Apparently, the results were "encouraging."[8]The equipment kept the beavers away, although they returned as soon as it was turned off. It also worked on ducks and geese, although they had some problems with infrared waterfowl detection. The birds would usually take flight when the equipment turned on, although if it was cold enough, they'd just sluggishly paddle away.

So electrofishing equipment probably can't help you catch blue whales. However, if you're having trouble keeping them out of your backyard pond ...

... it's possible the Denver Wildlife Research Center can help you out.

Earth’s atmosphere is really thin compared to the radius of the Earth. How big a hole do I need to dig before people suffocate?

—Sam Burke

The idea here is straightforward: When you dig a hole in the ground, the hole fills up with air.[1]The dirt you pile up outside the hole displaces air, so at first you won't have much effect on the surrounding atmosphere, but the effect grows as the hole gets deeper and the pile gets higher. So keep at it! If you dig a big enough hole, most of the atmosphere will flow in, and there won't be enough left outside the hole to breathe.[2]You need to remove about 65% of the atmosphere before sea level air becomes too thin to support human life.⁠[3]As this paper points out, it's odd—and likely coincidental—that the highest point on Earth happens to be just about exactly as high as the human high-altitude survival limit.

The atmosphere's exact volume is tricky to define, since it gets thinner at higher altitudes and doesn't have a firm boundary. If you compressed the whole thing to the density of normal surface air, it would be about 10 kilometers thick, and take up a volume of 4 billion cubic kilometers. 4 billion km³ of air is enough to fill a cube 1,000 miles high, which is nearly the volume of the solid core of the Earth. That gives us a rough idea of the scale of our hole.

Digging a hole that big will be a challenge. Even a hole the size of Massachusetts would have to be deeper than the diameter of the Earth to fit the whole atmosphere at surface pressure. A hole the size of the entire United States would need to be 400 kilometers deep, much deeper than we could actually dig.[4]And if you tried to dig up the entire surface of the United States to any depth, people would probably yell at you.

But wait! Air pressure changes with height. Air pressure goes down as you rise upward, which you can sometimes notice when your ears pop while driving on a hill or riding in a tall elevator. By the same token, pressure rises when you go downward. The air pressure in a deep mine is much higher than the pressure at sea level.

It might seem like the increasing pressure would help us fit more air into the hole. The pressure should compress the air, so a deep hole should be able to fit more than its "fair share" of air. But it doesn't quite work out that way.

As you go deeper into the Earth, the rock gets hotter.[5]Citation: Amiel, J., Eckhart, A. E., Swank, H., (2003) The Core Under the ideal gas law, pressure compresses air, but heat causes it to expand. In the case of a hole in the Earth's crust, the expansion from the heat of the rocks can actually counteract the compression from the higher pressure. Calculations in this paper⁠[6]This one is an actual paper and not a trailer for a terrible movie, I promise. show that temperature gradients of more than about 30°C per kilometer will result in no compression at all. If the temperature change is faster than that—as is common in areas with thin crust or volcanic activity—the density of air will actually drop as you go deeper, even as the pressure increases.

What if we compress the air some other way?

Diving tanks can contain air crushed by a factor of 200. A pile of diving tanks would only have to be a few hundred miles high to hold the entire atmosphere. If we want to compress air further, we can liquify it. Air is mostly oxygen and nitrogen. If we get air cold enough, it turns to a liquid with a density similar to water.

If we liquified the whole atmosphere—and for the record, I don't think we should—we could conceivably fit it all in the ground. We'd effectively need to remove a patch of the Earth's upper crust, exposing magma veins and pressurized chambers, and we'd have to somehow seal all those off and keep things cool enough that our storage tanks didn't melt.

The excavation would be a near-impossible challenge. But if you somehow solved all the countless engineering problems, you could—in principle—fit the entire liquified atmosphere of the Earth in a 5-mile-deep hole roughly the size of Texas.

Although you may not want to use that particular state.

What if the entire continental US was on a decreasing slope from West to East. How steep would the slope have to be to sustain the momentum needed to ride a bicycle the entire distance without pedaling?

—Brandon Rooks

Too steep to actually build, sadly. But for the next best thing, I suggest a vacation to the Hawaiian island of Maui.

First, the physics. Bikes coast downhill. On a long enough slope, a bike will reach a certain steady coasting speed. On a steep hill, their coasting speed will be faster, and on a gentle slope, they coast more slowly. If the slope is small enough, the bike will slow down and stop.

The shallowest slope at which a bike will still roll steadily forward is determined by the bike's coefficient of rolling resistance. In fact, the formula for this minimum slope—measured in terms of vertical drop over horizontal distance—is incredibly simple:

\[ \text{Minimum slope} = \text{Coefficient of rolling resistance} \]

"Slope equals coefficient of friction"[1]Sliding friction and rolling resistance work in different ways, but the coefficients are equivalent in these types of problems. If you want to be precise, you could use the phrase "coefficient of resistance" for all of them, but "coefficient of friction" is the more common term. is a handy general rule in physics: The coefficient of friction between an object on a surface is just the shallowest slope at which the object slides.[2]The coefficient of static friction is the slope at which the object starts sliding. The (usually lower) coefficient of dynamic friction is the minimum slope at which it keeps sliding once you give it a nudge.

For a nice bike under good conditions, the coefficient of rolling resistance can get as low as 0.002, or 1/500.[3]You can browse some test data here. That means that to travel 500 miles horizontally, you'll need a vertical drop of at least 1 mile. To travel the roughly 2,500 miles from New York to LA, you'd need to start off at least 5 miles up, higher than North America's highest mountain. I suggest bringing oxygen tanks.

But be warned—the trip could take a while.

A bike's rolling resistance mainly comes from the way the tire[4]And the ground, if you're riding on dirt.​[5]And the spokes and frame, if your bike is made of soft clay or something.​[6]Why do you have a bike made entirely of soft clay? deforms as it rolls, and it doesn't depend that much on how fast you're going. Air resistance, on the other hand, increases as you speed up, and under most conditions is the main drag force acting on a moving bike. To figure out how fast a bike will coast on a downhill slope, you need to calculate the point at which air resistance balances out the forward pull from gravity. At that point, the bike will stop accelerating. We can do that by using the formula for air resistance:

\[ \text{Forward pull from gravity} = \text{Rolling resistance} + \text{Drag force} \]

\[ m g \sin(\theta) = g \cos(\theta) C_r m + \tfrac{1}{2} C_d \rho A V^2 \]

\[ V = \sqrt{\frac{m g \sin(\theta) - g \cos(\theta) C_r m}{ \tfrac{1}{2} C_d \rho A}} \]

(V is the speed of the bike, C_r and C_d are the coefficients of rolling resistance and air drag, θ is the slope angle, g is the acceleration of gravity, m is the mass of the bike and rider, A is the frontal area of the bike and rider, and ρ is the density of air.)

For a very shallow slope of 0.2° or 0.3°, the bike would barely roll, and its top speed would be slower than a walking pace. You would need to add an extra few tenths of a degree to get the speed high enough to balance comfortably, and this would make the LA end of the slope even higher than the already implausible five miles.

But still, bicycles are pretty impressive coasting machines.[7]Trains have steel wheels which roll on smooth rails, so they should have very little rolling resistance. You can work out their coefficients by looking over technical specs or calculating from first principles, but a cleverer way is by watching train-pulling athletic events. Then, with a little calculation involving the limits of human strength and/or direct measurement, you can work out the coefficient from the other end. It turns out that train cars—at least, the kind used in strongman events—have coefficients of rolling resistance barely equal to that of a good bicycle. Skis, which are pretty good at sliding, actually have a coefficient of friction about 10 times higher than a bike's rolling resistance.

To ski from LA to New York, a skier would need to start off 10 times higher than a bike to make the same trip. Instead of the top of a mountain, they would need to start from near the edge of space. Not only is there no way to build a slope that tall, but ice isn't even stable at those low temperatures, so there'd be nothing to slide on.

In practice, the longest horizontal distance you could travel on a bike with an ideal ramp is probably not more than a couple hundred miles, and that would require ideal conditions. In the real world, the longest such trip might[8]It's billed as the longest, but I wonder if there's a longer one in some random stretch of gently-sloping downhill road in rural Mongolia or something. be the Haleakala downhill bike ride, which allows you to take a 35-mile trip from near the 10,000-foot summit all the way down to sea level with virtually no pedaling required.

(And if you can't make it to Maui yourself, you can at least enjoy the video search results for bicycle into water.)

Would a toaster still work in a freezer?

—My Brother, My Brother and Me, Episode 343, discussing a Yahoo Answers question

On a recent episode of Justin, Travis, and Griffin McElroy's terrific advice podcast, My Brother, My Brother and Me, the brothers pondered a Yahoo Answers question about what would happen if you put a toaster inside a freezer. (The discussion comes around the 36-minute mark.)

They have a fun discussion of a few aspects of the problem before eventually moving on to the next question. Since they don't really settle on a final answer, I thought we could help them out by taking a closer look at the physics of freezer toasters.

(A quick safety note: If you actually do this, keep in mind that the toaster may melt some of the ice in the freezer, leaving you with a running electrical appliance in a pool of water.)

Griffin sums up the situation like this:

You put a toaster in a freezer. You run the extension cord in there. You put some good bread in there. You click it down. What even happens, right? Because if your answer is, "it would get hot," then the freezer hasn't done its job. But if you say "it would get cold," then the toaster hasn't done its job.

For starters, the answer: The toaster would win. The freezer wouldn't do its job. Toasters beat freezers.

It's easy to think of a toaster and freezer as equivalent—one cools things down and the other warms them up. But toasters heat things up a lot more than freezers cool them down.

The coils in regular toasters get hot enough to glow, which means they're over about 600°C. Since the toaster is operating at such high temperatures, it would hardly notice whether the surrounding environment is 20°C (room temperature), 4°C (a fridge), or -15°C (a freezer).[1]The zero on our usual temperature scales can confuse things, since it makes it seem like going from 10° to 20° is "doubling" the temperature. But the "zero" on the Celsius scale is just a point chosen by convention. If we switch to Kelvin, which counts in degrees above absolute zero, a freezer is 260 K, a fridge is 275 K, a normal room is 295 K ... and the heating element in a toaster is 900 K.

The toaster needs to heat its coils from room temperature to somewhere over 600°C. From the toaster's point of view, a 20- or 40-degree change in starting temperature hardly matters. The coils will get hot, and then the bread will get hot, too. If the bread is colder at the start, the toaster will have to heat it a little longer to get it up to ideal toasting temperature, but it will have no trouble getting there. As anyone who's ever burned a piece of toast knows, toasters are definitely capable of heating bread to above the ideal temperature for toast.

In their discussion, the McElroys brought up another question: Even if the toaster can still toast bread at first, would it struggle to stay warm over time? If you left both the toaster and the freezer running, who would win in the long term?

The answer is that the toaster would still win. A toaster produces about a thousand watts of heat, and the cooling system in a household freezer can't remove heat that fast. In fact, since freezers are so well insulated, the inside of the freezer would probably get much hotter than the rest of the house, and eventually the toaster and/or the freezer would probably overheat.[2]Either device have a safety cutoff that stops things from actually melting down, but it's probably not wise to count on that in this situation.

Refrigerators and freezers work by soaking up heat from their interior and dumping it out the back.[3]That's why the area behind your freezer is warm, and why you can't cool a room by leaving the fridge door open. In a sense, they're more efficient than toasters. Fridges have a "coefficient of performance" of 2 or 3, which means it only takes them 1 unit of electrical energy to move 2 or 3 units of heat energy from the interior to the exterior. A toaster, on the other hand, produces 1 unit of heat from 1 unit of electricity. But since the compressor in a fridge-freezer typically only uses 100 or 150 watts when it's running,[4]You can see some real-world graphs of refrigerator power usage, courtesy people with home electricity meters, with a simple Google Image search. The distinctive on-off square-wave pattern is the compressor switching on and off throughout the day, while the big spikes are the heating element that keeps frost from building up on the coils. This power consumption is split between the fridge and the freezer, but if the fridge is already cold, most of the energy will be spent fighting with the toaster. so even with the efficiency multiplier, it can't keep up with the toaster's 1000+ watts of heat production.

Eventually, the toaster will start to heat up the inside of the freezer. Even if the freezer were as powerful as the toaster, it wouldn't be able to keep the toaster coils themselves from getting hot and toasting bread. The freezer can make the air around the toaster cold, but remember, to the toaster, all our air is cold.

If you happen to live in the Canadian city of Winnipeg, you can check this experimentally. The winter temperature at night in Winnipeg is about the same as the inside of a freezer, so the environment there effectively simulates a freezer with infinite capacity to absorb heat. Suppose you put a toaster out on your porch one night, plugged in by an extension cord, and leave it running for a few hours, going outside every so often to collect the toast and put in some fresh bread. What will happen? Simple: You'll quickly be eaten by wolves.

But assuming you survive the experiment, you should find that the toaster doesn't have trouble working in the cold air. It may take a bit longer to get the bread properly browned, but unless the wind is extremely strong, it should be able to manage it fine. After all, to a toaster, all weather is cold.

The difference between what humans consider "cold" and "warm" is negligible in a lot of high-temperature processes. For example, Antarctica has a well-equipped fire department. It might seem strange to worry about things getting too hot in the coldest place on Earth, but fire poses a serious threat to the researchers there. After all, the place is dry, windy, and doesn't have a lot of liquid water sitting around to douse a flame with. Sure, it's cold—but to a fire, everything is cold.

On the other hand, there are no wolves in Antarctica. So as long as you don't mind a trip—and you get clearance from the Antarctica fire department—you can go there to enjoy your outdoor freezer toast in peace.